One of the most important things people like about QlikView is that it is fast. A typical QlikView application usually takes less than a second to respond to a user selection (query), regardless of how you design the data model or write expressions. However, as data volume grows, tuning data model and expressions makes a huge difference in application performance.
The Usual
You probably have read quite a lot of best practices on performance tuning before. Let’s first get these relatively well known “usual” techniques out of the way so that we can discuss more interesting insights. “The usual” techniques include:
- Reducing data volume. The most common thing I have seen is people keep large amount of historical data in their applications. Maybe we should ask ourselves if it is really necessary to keep 10 years worth of data.
- Pre-calculating most frequently used expressions. For instance, if lots of charts are about Last Year Sales, instead of using on-the-fly calculation to dynamically figure out last year’s sales, maybe we should populate a new Last Year Sales field in the data model. Sometimes these expressions can be pre-calculated as flags;
- Pre-aggregating fact tables. If most charts are presenting data at a fairly high level, maybe we can create an aggregate table for the charts and only use detail level table when users want to view detail information. This way all charts are calculated quickly;
- Merge tables. When a query involves multiple tables, QlikView joins these tables on the fly through keys. Less tables means less joins and therefore faster response;
- Avoid string comparison. String comparison is very expensive in QlikView and it should be avoided as much as possible;
- Avoid big listboxes or tables boxes. Believe it or not, many people put listboxes or table boxes with millions of rows on the QlikView interface without know the tremendous system resources these objects consumes;
- Avoid showing too many objects at the same time. Having too many objects not only takes time to calculate these objects, but also takes time to download these objects to end user’s browser;
More Interesting Insights
I have often seen developers who follow the above best practices still run into performance issues. Based on my experiences the most commonly seen in-efficiencies are single-threaded calculations, many-to-many link keys, and in-proper use of Set Analysis / If functions.
Avoid single-threaded calculations
A single-threaded calculation can only be completed by one processor, regardless of how many processors QlikView Server has. Single-threaded calculations often cause long user waiting time when data volume gets bigger. For instance, on a QlikView Server that has 32 processors, a single-threaded calculation could takes 32 seconds to finish while the same calculation only takes 1 second if it’s written in a way that can run on multiple processors (aka a multi-threaded calculation). It gets even worse if hyper-threading is turned on for the QlikView Server.
What kinds of calculations are single-threaded? To answer this question, we need to understand why a single-threaded process happens. When QlikView evaluates a calculation, it needs to determine if it is mathematically possible to divide the calculation into small pieces, send individual pieces to different processors, and at the end combine results returned by processors into final results. If the answer is yes, then the calculation is multi-threaded. For instance, if we look at a simple expression of sum(Sales), it is possible to chop the table into pieces and send each piece to one processor to calculate sum(Sales) just for that piece. At the end QlikView can add the numbers from all processors up to get sum(Sales) for the entire table. However, if you look at an expression like count(distinct OrderID), you cannot cut the table into pieces, perform count(distinct OrderID) for each piece, then add them up, because different pieces might have common OrderIDs. Therefore count(distinct OrderID)must stay on one processor, making it a single-threaded calculation.
The most common single-threaded processes in QlikView are count distinct and macros. However, given how complex QlikView expressions can get, it is often not realistic for a developer to use the theory in the last paragraph to tell if an expression is single-threaded. The easiest way to find out is by checking the windows task manager to see how many processors are being used while the calculation is being processed by QlikView.
Once we determine there is an in-efficient single-threaded expression, various techniques can be used to make it multi-threaded. The most commonly used technique is to simplify the expression by creating new fields in the data model. For instance, in the above expression count(distinct OrderID), assuming OrderID is a unique key (aka perfect key in QlikView) in its table, we can create a new field called OrderIDCounter and always assign 1 to this field. The expression is therefore changed to sum(OrderIDCounter), which can easily be distributed to multiple processors. Unfortunately there’s no one-size-fits-all solution, each expression needs to be reviewed separately to determine the best way to improve it.
Set Analysis vs. If function
Set Analysis and If function are interchangeable in many cases. Many people often wonder which one is faster. Well, in most cases Set Analysis is more efficient because it takes advantage of pre-built in-memory indexes while an if function in an expression that often causes a full table scan. For example, to calculate the sales in a shoe department, you can either use sum({<Department={“Shoe”}>} Sales) or sum(if(Department=’Shoe’, Sales)). The first expression uses indexes to go right to the portion of the table that contain Shoe while the second expression does a full table scan and examines each record to determine if it belongs to Shoe.
You probably wonder why I said “in most cases” instead of “always” when I declare Set Analysis is more efficient. It is true that sometimes an If function can be just as or even faster than Set Analysis. This is because when a large portion of the table meets the criteria, the time spent on checking indexes could out-weigh the saving in latter calculations. Using sum({<Department={“Shoe”}>} Sales) and sum(if(Department=’Shoe’, Sales)) as an examples again, if more than 20% of the records in Sales table belong to Shoe, then the if function might have an advantage because it takes time for the Set Analysis expression to use indexes to figure out what records of the fact table contains Shoe data.
Avoid many-to-many key links
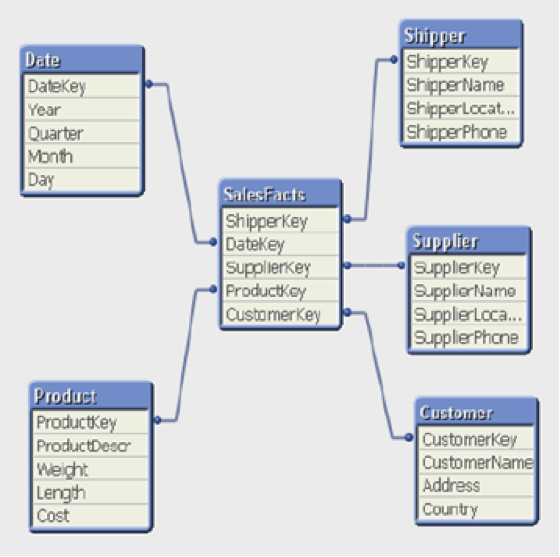
QlikView pre-calculates all of the links among tables so that it is fast when tables are joined to calculate an expression. However, this is truer if every link key is a perfect key in one of the tables it connects. For instance, in the data model below, ShipperKey links Shipper and SalesFacts tables and the closer ShipperKey is to a perfect key in table Shipper, the faster the join can be calculated. When ShipperKey is a perfect key in Shipper, each record in Shipper is linked to multiple records in SalesFacts, making the link to be one-to-many, which is ideal for QlikView.
If the key field linking two tables is not a perfect key, then each record in either table is linked to multiple records in the other table (many-to-many), this is very in-efficient in QlikView.